Languages
Natural languages
- We use natural languages to communicate with each other.
- Syntax and grammar rules determine valid word order.
- Semantics determine what a group of words ‘means’.
- Syntax can be fine, but the semantics can be bad.
- The petrol ate the car
- One statement could be ambiguous—have multiple meanings
- Bath the dog wearing an apron.
Formal Languages
-
Formal languages are much more carefully defined than a natural language.
-
As a result, ambiguity is not possible.
-
Some formal languages include:
- Chemical formulae
- Maths
- Programming languages
Reverse Polish Notation (RPN)
Infix Notation
- When we look at mathematical expression the operands are placed on either side of the operator.
- 3+4
- The operand being the data we want to use and the operator being what we want to do with it
- This is infix notation
- The problem is that we often need brackets to alter the order of operations.
- (5+7) x 3
RPN
-
Polish mathematician Jan Łukasiewicz devised a way to represent mathematical expressions so that we don’t need to use brackets
-
This uses postfix notation so the operator is shown after the items we need to operate on
- 3 4 +
-
The result of an operation replaces the items that caused it to happen in the expression.
- 5 7 + 3 x ⇒ 12 3 x ⇒ 36
-
Representing calculations in reverse polish makes it easier for machines to interpret.
-
In particular, calculations express in RPN take less steps to process on a computer.
-
To perform an RPN calculation, we use a stack.
RPN and the Stack
-
Here’s an infix notation:
- 5 x ( 1 + 2)
-
Represented as RPN it looks like
- 1 2 + 5 x
-
In operation
- Push 1 and 2
- Pop 2, 1 and add.
- Push 3 (result of add)
- Pop 3,5 and multiply.
- Push 15 (result of multiply)
-
Stack now contains the result
RPN as a Tree
- You can also represent RPN as a tree.
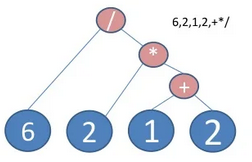
- The tree can be reversed post order with each calculation replacing the operator.
Regular Expressions
- A regular expression provides a way to define sequences of characters
- The regular expression can then be used to pattern match
- To find examples in a bigger body of characters
- To determine if an input matches an allowed pattern
- The regular expression defines the whole set