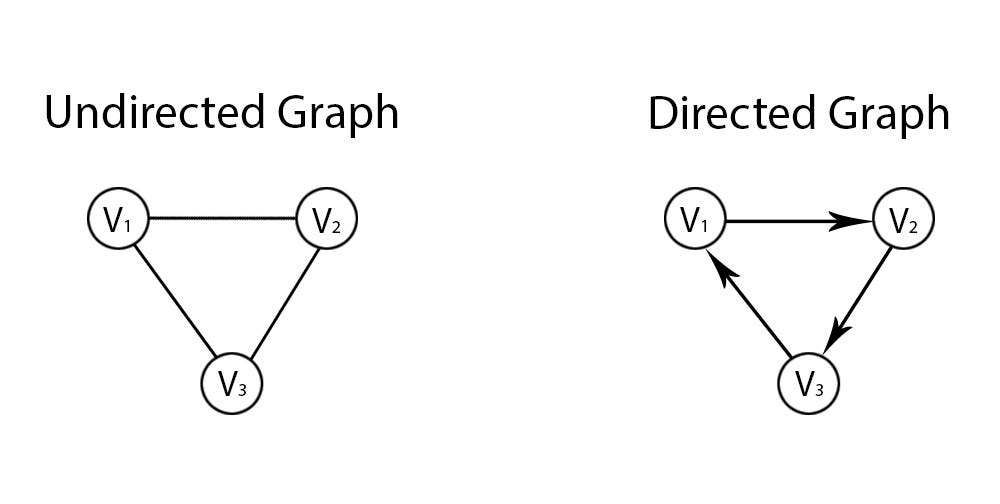
Graphs are used to represent data visually. They require relations between the data.
Circles or nodes are called vertices and the lines between them are called edges.
Larger graphs might look like this:
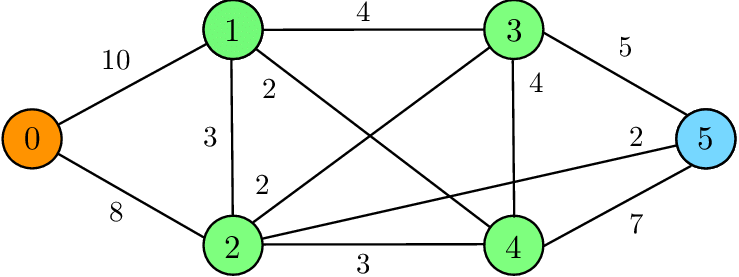
 If an edge has a value associated with it, such as 6, then that edge is weighted. Typically, if one edge is weighted, you would expect all other edges to have a weight. You can describe a graph that includes weights, intuitively, as a weighted graph.
If an edge has a value associated with it, such as 6, then that edge is weighted. Typically, if one edge is weighted, you would expect all other edges to have a weight. You can describe a graph that includes weights, intuitively, as a weighted graph.
You can also represent data from a graph as an adjacency matrix
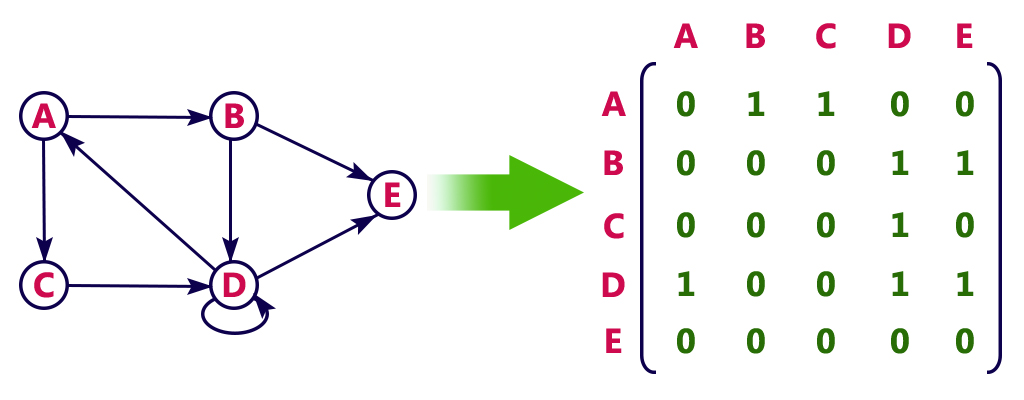
If a graph would be symmetrical, so all weighted values are equivalent both ways (so A to B and B to A both have a value of 5), then you only need to complete half of the graph, giving you a triangular shape to your adjacency matrix.
The graph below only defines one value for each route, meaning it would be symmetrical.
Data can also be represented as an adjacency list, such as the one shown below.
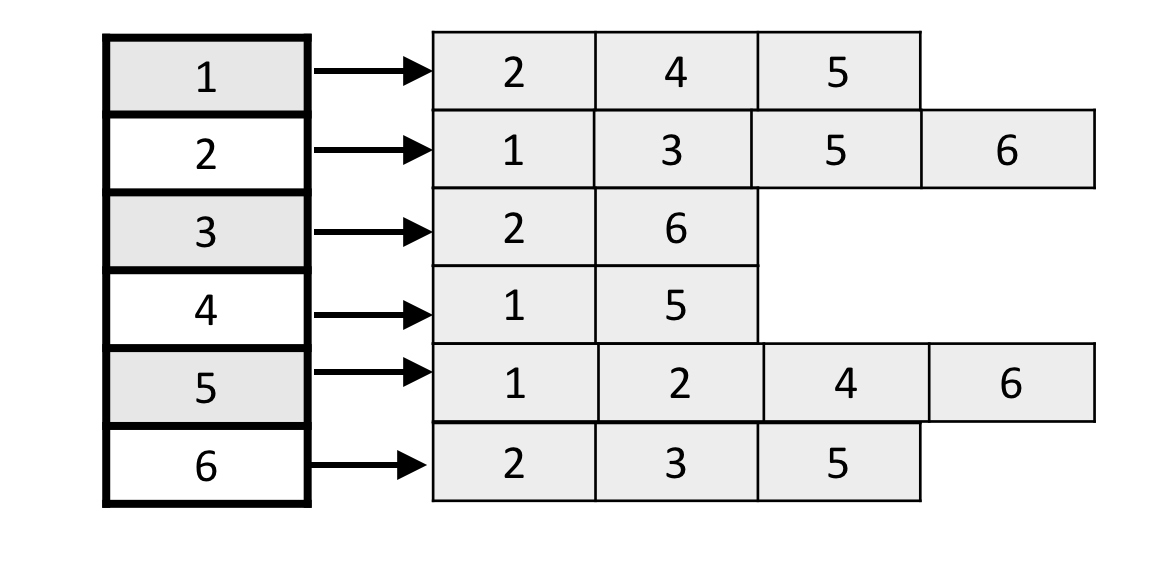
An adjacency list makes more sense when there are few connections between vertices as it will use less space.
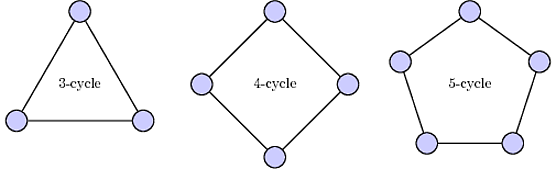
A cycle occurs if you can move from a vertex without crossing an edge twice.
A tree is another kind of graph.
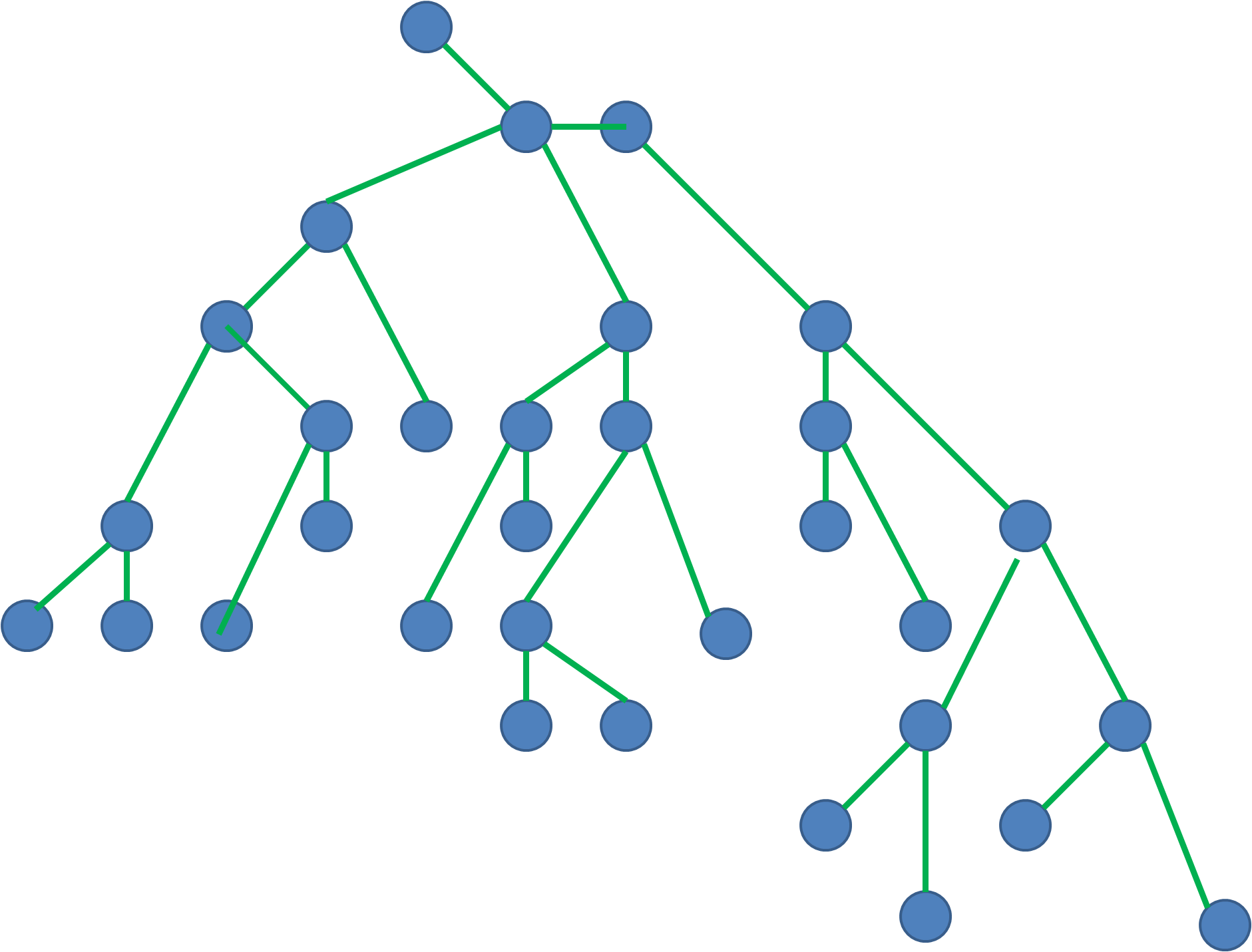
To be a tree, a graph must:
- have no cycles
- be fully connected (one structure)
- cannot be directed or weighted
A tree will have a root, which is designated.
The vertexes at the end of a tree are called leaves, whilst the edges between vertexes are called branches.
Binary Trees
Constructing a tree
-
We take the data in the order that it arrives in and add it to the tree
-
If the tree already has a vertex, then we have to compare the data to the previous entry.
-
If the data comes BEFORE the previous vertex, we create a vertex to the left of the vertex. If it comes AFTER the previous vertex, we create a vertex to the right of the vertex.
-
A tree is typically more efficient than trying to sort your data.
-
Usually used for smaller datasets and stored in RAM
Tree traversal
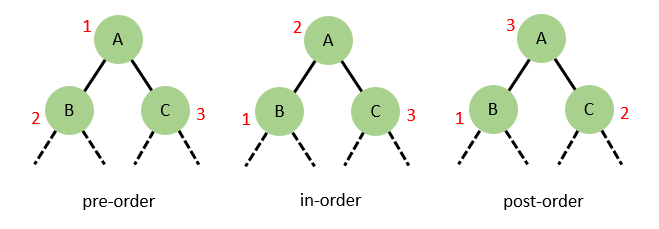
Pre-order
-
Process the root of the tree first
-
Then the left branch of the tree
-
Then the right branch of the tree
-
Uses:
- copy
In-order
-
Process the left branch first
-
Then the root
-
Then the right branch
-
Uses:
- sort
Post-order
-
Process the left branch first
-
Then the right branch
-
Then the root
-
Uses:
- delete
- Process is different depending upon what the program is doing
- When moving down a tree, you effectively create sub-trees, which have their own root. You use this to repeat the traversal process down the tree.
And time for the beautiful hand-drawn tree, with sorted examples.

Storing a binary tree
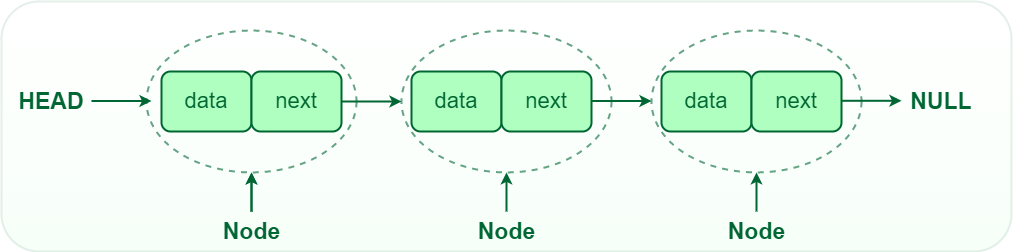
- You could use an adjacency matrix or list, however a linked list is the proper method.
Linked list
- Items do not have to be next to each other in memory, unlike an array.
- A pointer simply indicates where each item is stored in memory.
Polynomials
- Better than exponentials
Exponential
- O(x^n)
(In)Tractable
- Intractable
- We know how to solve the problem
- We could write code to solve the problem
- However the code would not complete in a reasonable amount of time
Noncomputable
- There is no known solution for the problem